Srinivasa Ramanujan ~ Computer Technology

Mathematical achievements

In mathematics, there is a distinction between having an insight and having a proof. Ramanujan's talent suggested a plethora of formulae that could then be investigated in depth later. It is said that Ramanujan's discoveries are unusually rich and that there is often more in it than what initially meets the eye. As a by-product, new directions of research were opened up. Examples of the most interesting of these formulae include the intriguing infinite series for π, one of which is given below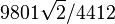

$\frac{1}{\pi} = \frac{2\sqrt{2}}{9801} \sum^\infty_{k=0} \frac{(4k)!(1103+26390k)}{(k!)^4 396^{4k}}.$

This result is based on the negative fundamental discriminant d = −4×58 with class number h(d) = 2 (note that 5×7×13×58 = 26390) and is related to the fact that

$e^{\pi \sqrt{58}} = 396^4 - 104.000000177\dots.$

Compare to Heegner numbers, which have class number 1 and yield similar formulae. Ramanujan's series for π converges extraordinarily rapidly (exponentially) and forms the basis of some of the fastest algorithms currently used to calculate π. Truncating the sum to the first term also gives the approximation $9801\sqrt{2}/4412$ for π, which is correct to six decimal places.
One of his remarkable capabilities was the rapid solution for problems. He was sharing a room with P. C. Mahalanobis who had a problem, "Imagine that you are on a street with houses marked 1 through n. There is a house in between (x) such that the sum of the house numbers to left of it equals the sum of the house numbers to its right. If n is between 50 and 500, what are n and x." This is a bivariate problem with multiple solutions. Ramanujan thought about it and gave the answer with a twist: He gave a continued fraction. The unusual part was that it was the solution to the whole class of problems. Mahalanobis was astounded and asked how he did it. "It is simple. The minute I heard the problem, I knew that the answer was a continued fraction. Which continued fraction, I asked myself. Then the answer came to my mind", Ramanujan replied.
His intuition also led him to derive some previously unknown identities, such as

$\left [ 1+2\sum_{n=1}^\infty \frac{\cos(n\theta)}{\cosh(n\pi)} \right ]^{-2} + \left [1+2\sum_{n=1}^\infty \frac{\cosh(n\theta)}{\cosh(n\pi)} \right ]^{-2} = \frac {2 \Gamma^4 \left ( \frac{3}{4} \right )}{\pi}$

for all

θ

, where

Γ(z)

is the gamma function. Equating coefficients of

θ 0

θ 4

, and

θ 8

gives some deep identities for the hyperbolic secant.
In 1918, G. H. Hardy and Ramanujan studied the partition function P(n) extensively and gave a non-convergent asymptotic series that permits exact computation of the number of partitions of an integer. Hans Rademacher, in 1937, was able to refine their formula to find an exact convergent series solution to this problem. Ramanujan and Hardy's work in this area gave rise to a powerful new method for finding asymptotic formulae, called the circle method.^[81]
He discovered mock theta functions in the last year of his life. For many years these functions were a mystery, but they are now known to be the holomorphic parts of harmonic weak Maass forms.

[edit] The Ramanujan conjecture

Main article: Ramanujan–Petersson conjecture

Although there are numerous statements that could bear the name Ramanujan conjecture, there is one statement that was very influential on later work. In particular, the connection of this conjecture with conjectures of André Weil in algebraic geometry opened up new areas of research. That Ramanujan conjecture is an assertion on the size of the tau function, which has as generating function the discriminant modular form Δ(q), a typical cusp form in the theory of modular forms. It was finally proven in 1973, as a consequence of Pierre Deligne's proof of the Weil conjectures. The reduction step involved is complicated. Deligne won a Fields Medal in 1978 for his work on Weil conjectures.^[82]

[edit] Ramanujan's notebooks

Further information: Ramanujan's lost notebook

While still in India, Ramanujan recorded the bulk of his results in four notebooks of loose leaf paper. These results were mostly written up without any derivations. This is probably the origin of the misperception that Ramanujan was unable to prove his results and simply thought up the final result directly. Mathematician Bruce C. Berndt, in his review of these notebooks and Ramanujan's work, says that Ramanujan most certainly was able to make the proofs of most of his results, but chose not to.
This style of working may have been for several reasons. Since paper was very expensive, Ramanujan would do most of his work and perhaps his proofs on slate, and then transfer just the results to paper. Using a slate was common for mathematics students in India at the time. He was also quite likely to have been influenced by the style of G. S. Carr's book, which stated results without proofs. Finally, it is possible that Ramanujan considered his workings to be for his personal interest alone; and therefore only recorded the results.^[83]
The first notebook has 351 pages with 16 somewhat organized chapters and some unorganized material. The second notebook has 256 pages in 21 chapters and 100 unorganized pages, with the third notebook containing 33 unorganized pages. The results in his notebooks inspired numerous papers by later mathematicians trying to prove what he had found. Hardy himself created papers exploring material from Ramanujan's work as did G. N. Watson, B. M. Wilson, and Bruce Berndt.^[83] A fourth notebook, the so-called "lost notebook", was rediscovered in 1976 by George Andrews.^[2]

^{READ MORE HERE}